Postprocessing

Socio-economic surplus

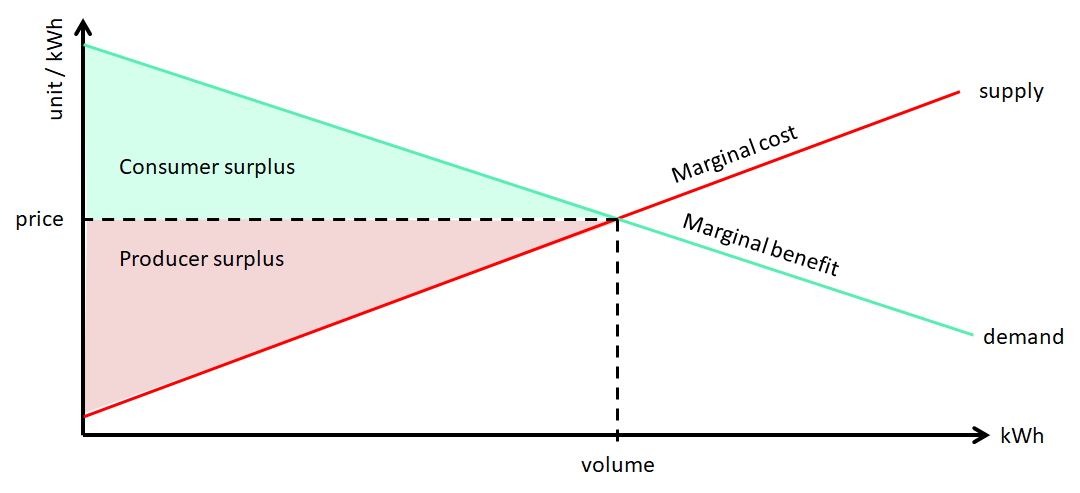
The socio-economic surplus (SES) is calculated as the sum of consumer surplus (\( \textit{CS} \) ) and producer surplus ( \( \textit{PS} \)), as illustrated below. Sketch socio-economic welfare calculation

In our calculation of SES we also calculate the difference in water filling ( \( WF \) ) and congestion rent on transmission corridor ( \( \textit{T} \) ), which is considered a part of the consumer surplus.

Mathematical description

The following mathematical description divides the calculation of socioeconomic welfare in different parts. Each of the defined assets / technologies provides a function to calculate its profit margin \(\Pi(k)\) at time step \(k\). The sum over all profit margins is the socio-economic welfare.

  • \(p(k)\) - production of a unit at time step \(k\)

  • \(\lambda(a,k)\) - power price in the respective area \(a\)

Thermal production

For all thermal plants and all timesteps \( k \):

\[ \textit{CS} \mathrel{+}= p(k) * [\lambda(a,k)-MC(k)] \]

Where \(MC(k)\) is the marginal production cost.

Intermittent RES - wind, solar

For all wind parks, solar parks and all timesteps \( k \):

\[ \textit{PS}_\textit{res}(k) \mathrel{+}= p(k) * \lambda(a,k) \]

Market steps

For all market steps and all timesteps \( k \):

\[ \textit{PS} \mathrel{+}= d(k) * [\lambda(a,k) - \textit{Cost}(k)], \textit{if } d(k) > 0.0 \]
\[ \textit{CS} \mathrel{+}= d(k) * [\textit{Cost}(k) - \lambda(a,k)], \textit{if } d(k) < 0.0 \]

Where \( Cost(k)\) is the cost of the market step.

Firm consumption (incl. price elasticity)

The consumer surplus is also adjusted by price elasticity defined with the segments \(x \in \mathbb{X}\).

The segments have:

  • a defined capacity \(C_{e}(a, x,k)\)

  • a defined consumption \(c_{e}(a, x,k)\)

  • and a cost \(\textit{Cost}_{e}(a, x,k)\)

For all price elastic steps and all timesteps \( k \):

\[ \textit{CS} \mathrel{+}= [C_{e}(a, x, k) - c_{e}(a, x, k)] * [\textit{Cost}(a, x, k) - \lambda(a,k)], \textit{if } C(k) > 0.0 \]
\[ \textit{CS} \mathrel{-}= c(x, k) * [\textit{Cost}(x, k) - \lambda(a,k)], \textit{if } C(k) < 0.0 \]

The consumer surplus for firm demand \( D(a, k) \) is curtailed by price elasticity and consumed rationing:

\[ \textit{D}_{cur}(a, k) = D(a, k) - R_{consumption}(a, k) - \sum_{x \in X} C_{e}(a, x, k) \]

For all \( C_{e(a, x, k)} > 0 \).

Thus, for all areas and all timesteps \( k \):

\[ \textit{CS} \mathrel{+}= D_{cur}(a, k) * [R_{cost}(a, k) - \lambda(a, k)] \]

Battery

  • \(dis(k)\) - discharge of battery

  • \(chg(k)\) - charge of battery

For all batteries and all timesteps \( k \):

\[ \textit{PS} \mathrel{+}= (dis(k) - chg(k))*\lambda_{a,k}\]

Congestion rent on transmission corridors

The surplus for a transmission corridor, or congestion rent is calculated by the price difference of the connected areas and the flow. Prices in both ends of the line are defined as:

  • \(\lambda(a_{to},k)\)

  • \(\lambda(a_{fr},k)\)

The exchange on a transmission corridor from area \(a_{fr}\) to \(a_{to}\) is defined as \( exc(k) \), and the surplus is split between the two areas:

\[ T(a_{to})) \mathrel{+}= 0.5*exc(a_{to}, a_{fr}, k) * (\lambda_{a_{to},k} - \lambda_{a_{fr},k}) \]
\[ T(a_{fr})) \mathrel{+}= 0.5*exc(a_{to}, a_{fr}, k) * (\lambda_{a_{to},k} - \lambda_{a_{fr},k}) \]

If losses are defined for transmission, these need to be accounted for. Losses are distributed on both sides of the line. Losses on the corridor are defined as \(loss(k)\)

Both sides:

\[ T(a_{to}) \mathrel{+}= loss(k) * 0.5 * (\lambda(a_{to},k) + \lambda(a_{fr},k)) \]
\[ T(a_{fr}) \mathrel{+}= loss(k) * 0.5 * (\lambda(a_{to},k) + \lambda(a_{fr},k)) \]

Hydro power production

For all hydro power plants and all timesteps \( k \):

\[ \textit{PS} \mathrel{+}= p(k) * \lambda(a,k) \]

Water filling difference

For the calculation of the profit margin for hydro power a correction for the change in reservoir filling needs to be done. This is done by integrating over the reservoir filling and water value for each reservoir as:

\[ \textit{WF} = \int_0^X res(x, k_N) * WV(x, k_N) \, dx - \int_0^X res(x, k_0) * WV(x, k_0) \, dx \]

Where \(WV(x,k)\) is water value for module for all levels \(x\), \(res(x, k)\) is the amount of water at level \(x\). The reservoir volume is split into \( X \) number of levels, and each level is of size \( (V_\textit{max} - V_\textit{min}) / (X - 1) \), where \( V_\textit{max} \) and \( V_\textit{min} \) is the user provided maximum and minimum limits for the reservoir.

Total

Total socio-economic surplus is thus \( \textit{CS} + \textit{PS} + \textit{WF} + T \)

Code example

See the API refrence for more details.

# Required structures
run_config: RunConfig
logical_model: LogicalModel
input_ds: DataStore
result_ds: DataStore

# Perform a simulation
# ...

from trident_extras.post_processing import calc_socio_economic_surplus
import json

report = calc_socio_economic_surplus(run_config, logical_model, input_ds, result_ds)
print(report.to_ascii_table())
print(json.dumps(report.to_dict()))